ポケモンバトルの仲間大会*1にて、テツポンドさん主催の「いやしのはどう1on1」が開催されました。 私がこれに参加するにあたり、計算機によるシミュレーションを用いてどんなポケモンが強いか考察したので、その結果と手法を示します。
動機
私は以前よりポケモンファンではあるのですが、ポケモンバトルの経験はごく浅く、どんなポケモンが強いかということを自力で考察するだけのスキルがありません。 SNSで見かけた本大会は、通常のバトルと比べて選択肢が非常に狭いため、シミュレーションで最適解を求められるのではないかと考えました。 求まった解を検算することを通じて、バトルを考察するスキルの向上にもつながるのではないかと期待しました。
ルール
使用ソフトはポケットモンスター スカーレット・バイオレットで、2025年7月12日に開催されました。大会のルールを引用します。
(1) 覚えさせることができる技はいやしのはどうだけ (2) 禁止級伝説のポケモン及び幻のポケモンは禁止(ポケモンSVランクバトルレギュレーションF(2024年1月~4月)で使用できたポケモンたちならOK) (3) バトルチームへの登録は1匹のみ
いやしのはどうは、相手のHPを最大HPの1/2だけ回復するという効果であり、自分に不利に働く技です(本来、ダブルバトルで味方に使う技です)。実質的には、いやしのはどうのPPが切れた後に自動的に出るわるあがきによって攻撃することになります。わるあがきは威力50の技で、使用すると反動として自分のHPを最大HPの1/4だけ減らします。相手に大きなダメージを与えられれば有効ですが、ダメージが小さければ反動によって不利になるという性質があります。
求められた解
※わるあがきの反動を切り捨てで計算していたため、本来の挙動とわずかに異なります。末尾に修正後の再計算結果を掲載しています。
シミュレーションにより、実際に求められた解を示します。計算の前提条件は、手法の章をご覧ください。 パーティ構築は、以下の混合戦略ナッシュ均衡になりました。ガラルヤドランを出す参加者が29%、ブリムオンを出す参加者が19%…いれば、どの参加者も勝率50%になるということを示しています。この表にないパーティは、弱い選択肢となります。なお、ヤドンとガラルヤドンは全く同じパラメータであり、どちらでも構いません*2。
| 選出確率 | パーティ |
|---|---|
| 29.70% | ヤドラン(ガラル),チョッキ,H4,A252,B252,S0,A↑,S↓,最遅 |
| 19.53% | ブリムオン,チョッキ,H60,A252,B196,S0,B↑,S↓,最遅 |
| 13.98% | ヤドン(ガラル),チョッキ,H4,A252,B252,S0,B↑,S↓,最遅 |
| 12.73% | ヤドラン,チョッキ,H4,A252,B252,S0,B↑,S↓,最遅 |
| 9.49% | ヤドラン,チョッキ,H252,A4,B252,S0,B↑,S↓,最遅 |
| 8.72% | エルレイド,チョッキ,H4,A252,B252,S0,A↑ |
| 2.63% | ヤドラン(ガラル),チョッキ,H252,A4,B252,S0,B↑,S↓,最遅 |
| 2.16% | ブリムオン,チョッキ,H252,A4,B252,S0,B↑,S↓,最遅 |
| 1.06% | ヤドラン,たべのこし,H252,A4,B252,S0,B↑,S↓,最遅 |
凡例: チョッキ=とつげきチョッキ、H4, A252などは努力値配分、A↑は攻撃上昇性格補正、S↓は素早さ下降性格補正、最遅はすばやさ個体値0。原則個体値は最大。
持ち物のとつげきチョッキは、変化技を出せなくするという効果があります。いやしのはどうは変化技であるため出せなくなり、最初のターンからわるあがきを使うようになります。「いやしのはどう1on1」ではありますが、わるあがきしか使わない設定のパーティがほとんどとなります。
なお、バトル中の行動選択の余地はありません。パーティのポケモンが1体、覚えている技が1つだけかつ、テラスタルに意味はないと考えられるためです。
詳細
混合戦略ナッシュ均衡において製の確率が割り振られたパーティ間の利得行列は以下のようになります。利得1が勝率100%、-1が勝率0%を示します。
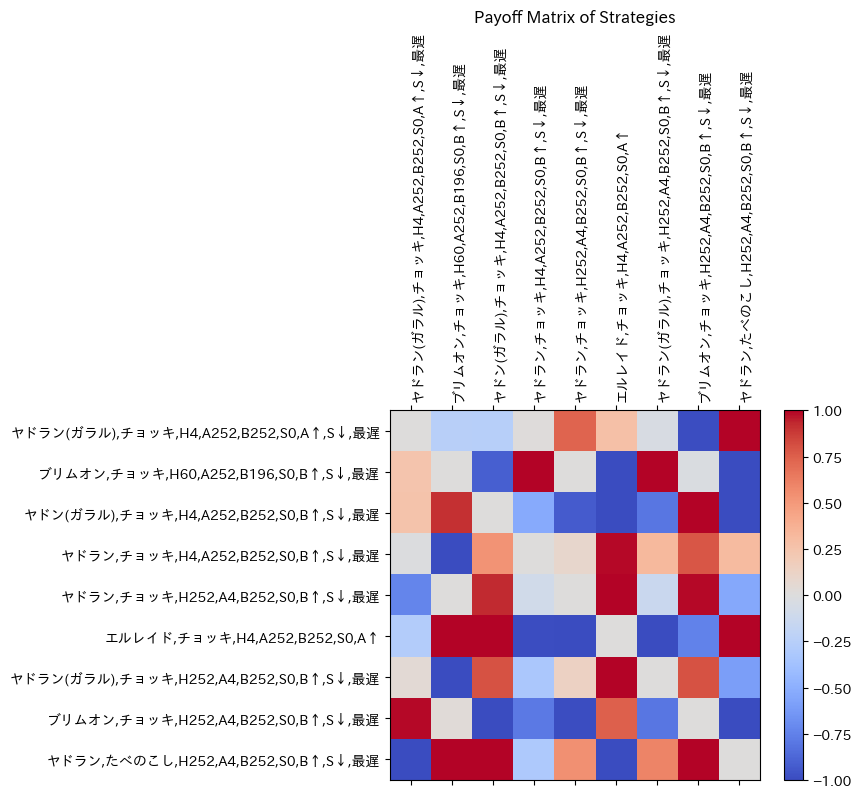
例えば、一番上の行のガラルヤドランは、8列目のブリムオンに不利、9列目のヤドランに有利です。 タイプ相性は関係がないルールですが、ポケモンのステータス配分により複雑な強弱関係が生まれています。 持ち物としてとつげきチョッキが多数派ですが、たべのこしも有効であることがわかりました。 なお、たべのこし型のポケモンの選択確率は1.06%ですが、確率が低いことは弱い・選ぶ価値がないことを意味しません。ナッシュ均衡下において、どのパーティも勝率は50%で均等です。
シミュレーションの方法
ここからは、上記の結果を得るまでの過程を紹介します。プログラムでシミュレーションを行うにあたって、ブラックボックスをなくし詳細を理解したいという意図から、ダメージ計算式等をすべて一から実装する方針を取りました。 ルール上ポケモンや技の数はかなり絞られていますが、持ち物は自由であり、あらゆる持ち物の挙動を実装するのは工数が多くかかります。 そのため、まずは手作業での環境考察を行い、プログラムでシミュレーションすべき範囲を絞りました。次に、シミュレーションプログラムを実装し、解を求めました。 アルゴリズムはごく単純で、生成AIや機械学習の要素はありません*3。
手作業での環境考察
参加可能なポケモン
まず、参加可能なポケモン(いやしのはどうを覚えられる、かつレギュレーションFに含まれる)は以下の34種類です。進化前ポケモンがいますが、素早さが低いことが有効な場合もあるため、すべて考慮に入れることとしました。
ピッピ, ピクシー, プリン, プクリン, ヤドン, ヤドン(ガラル), ヤドラン, ヤドラン(ガラル), ラッキー, チコリータ, ベイリーフ, メガニウム, ピィ, ププリン, ヤドキング, ヤドキング(ガラル), ドーブル, ハピナス, ラルトス, キルリア, サーナイト, チリーン, ラティアス, ラティオス, ルカリオ, エルレイド, ゴチム, ゴチミル, ゴチルゼル, ブロスター, ミブリム, テブリム, ブリムオン, イエッサン♀
持ち物
持ち物に関しては制約がないため、対戦において効果のある持ち物すべてを一度検討し、有効と考えられるとつげきチョッキとたべのこしをシミュレーションに含めることとしました。
とつげきチョッキ以外の持ち物では、10ターンの間いやしのはどうを使うことになります。あいてがとつげきチョッキを持っていて最初からわるあがきを使ってくる場合、そのダメージを受け、そしてわるあがきの反動(最大HPの1/4)はいやしのはどう(最大HPの1/2)で完全に回復されることになります。わるあがき10回分のダメージを耐えられなければ意味がありません。
(参加可能な中で最も攻撃が高い)攻撃特化エルレイドが(最も耐久性能が高い)防御特化ヤドランにわるあがきを打つと、1発あたりダメージが10.4%~12.4%となります。つまり、10発耐えられません。ダメージを軽減するか回復する持ち物が必要です。10ターンの間の回復量を考えると、1回だけ回復するきのみではなく、毎ターンHPを最大HPの1/16だけ回復するたべのこしが最も良いと言えます。毒タイプのポケモンの場合は、同等の効果を持つくろいヘドロでもよいです。
ゴツゴツメットは攻撃してきた相手に最大HPの1/6のダメージを与えますが、わるあがき使用者に1ターン当たりに与えられるダメージは最大HPの1/4+1/6であり、いやしのはどうで完全回復してしまうため、同様に採用しづらいです。
厳密には、攻撃特化エルレイドの相手をする必要性が薄いという結論もありうるため、ほかの持ち物が無意味であるという保証まではできませんでした。
特性
特性について考察しましたが、シミュレーションに含めるほど重要なものはないと判断しました。
有用そうな特性として、ドーブルが持つテクニシャンとムラっけがあります。テクニシャンは、わるあがきに効果がありその威力を1.5倍にします。ムラっけは、「毎ターン終了時、『こうげき』『ぼうぎょ』『とくこう』『とくぼう』『すばやさ』いずれかのランクが2段階上がり、別のランクが1段階下がる。」という効果です。ドーブルの種族値が低く、これらを持っても勝てる見込みがほとんどないと判断し、シミュレーションでこれらの特性は実装しませんでした。ムラっけについては、最初の3ターンで防御が上がり続け、次に攻撃が上がり続けるという非常に都合の良い乱数が生じれば、たべのこしを持たせて有力なポケモンを倒せますが、あまりに確率が低いです。
ピクシーが持つメロメロボディは、わるあがきを使用した相手を30%の確率でメロメロにできます。ただし、相手と性別が違っていないと発動しないため使いづらいです。また、最終的な実験結果から分かるように素早さが遅いほうが得なケースが多く、わるあがきを使って与えられるダメージより反動のほうが大きいという状況も多いと考えられ、行動不能によって1ターンパスできることは必ずしもデメリットではなさそうです。しいて言えば、攻撃種族値最大であるエルレイドは♂しかいないため、ピクシー♀を使うことで積極的にメロメロボディの発動を狙うことができます。
ガラルヤドランが持つクイックドロウは、「素早さに関係なく、30%の確率で同じ優先度の攻撃技を先制攻撃できる。」という特性です。最終的な実験結果においてガラルヤドランは最遅を狙う戦略が有効なため、先制できることで有利となるケースが極めてまれと考えられます。
シミュレーションプログラムの実装
コードはこちらにあります。16スレッドマシンで40分ほどかかります。
https://github.com/select766/pokemon-iyasi1on1
処理の概要は以下の通りです。
- ポケモンの種族×努力値配分×性格補正×持ち物の組み合わせでパーティを構築する。
- パーティ2つの組み合わせについて1000回対戦を行わせ、勝率を計算する。
- パーティ1つを1つの戦略と考え、混合戦略ナッシュ均衡を求める。
コードはPythonで実装しました。
パーティ候補の生成
ポケモンの種族は、参加可能な全ポケモン34種類を候補にします。
努力値配分と性格補正は、あらゆるパターンを考慮すると非常に多いです。今回は、以下の19通りに絞りました。
| No | 上昇性格 | 下降性格 | 努力値252 | 余り | 最遅 |
|---|---|---|---|---|---|
| 0 | A | AS | HB | ||
| 1 | S | AS | HB | ||
| 2 | B | AS | HB | ||
| 3 | A | A | HB | ||
| 4 | S | A | HB | ||
| 5 | B | A | HB | ||
| 6 | A | S | HB | ||
| 7 | S | S | HB | ||
| 8 | B | S | HB | ||
| 9 | A | HB | A | ||
| 10 | S | HB | A | ||
| 11 | B | HB | A | ||
| 12 | A | HB | S | ||
| 13 | S | HB | S | ||
| 14 | B | HB | S | ||
| 15 | A | S | A | HB | 1 |
| 16 | B | S | A | HB | 1 |
| 17 | A | S | HB | A | 1 |
| 18 | B | S | HB | A | 1 |
「努力値252」は努力値を最大の252まで振るパラメータです。余りには、努力値合計の508から、努力値252の列で使用しなかった分を振ります。HBについては、与えられた合計値を用いて、HPと防御の実数値の積が最大になるように配分を決定しました。ダメージ計算においては、相手の攻撃力が式に含まれ、整数の割り算で切り捨ての処理が含まれるためこの配分があらゆる状況で最適とまでは保証できません。個体値は原則最大で、最遅の場合は素早さの個体値を0にします。
持ち物はとつげきチョッキとたべのこしの2種類を実装しました。
これらすべての組み合わせで、34×19×2=1292通りのパーティ候補が計算されます。
バトルのシミュレーション
いやしのはどう・わるあがきのみの限定的な環境でバトルをシミュレートするコードを実装しました。ダメージおよび素早さが同じ場合の先攻・後攻がランダムとなるため、乱数を用います。ポケモンWiki等に掲載されているダメージ計算式を素直に計算するだけです。
def simulate(pokes: tuple[Poke, Poke], rng: random.Random) -> int: """ バトルをシミュレートし、勝者(0 or 1)を返す PokeのHPは変化するため、事前にreset()を呼んでおくこと。 """ while True: if pokes[0].s > pokes[1].s: move_order = [0, 1] elif pokes[1].s > pokes[0].s: move_order = [1, 0] else: # 同速なのでランダムに先攻を決める move_first = rng.randint(0, 1) move_order = [move_first, 1 - move_first] for attacker_idx in move_order: attacker = pokes[attacker_idx] defender = pokes[1 - attacker_idx] if attacker.heal_pulse_pp > 0: # いやしのはどうが発動 attacker.heal_pulse_pp -= 1 # 回復量は切り上げ # メガランチャーは考慮していない defender.current_hp = min( defender.max_hp, defender.current_hp + math.ceil(defender.max_hp / 2), ) else: # わるあがきが発動 damage = calc_damage( attacker.level, 50, # わるあがきの威力 attacker.a, defender.b, rng.randrange(0, 24) == 0, # 急所は1/24 rng.randrange(0, 16), # ダメージ乱数は16段階 ) defender.current_hp = max(0, defender.current_hp - damage) if defender.current_hp == 0: return attacker_idx # 反動 recoil = attacker.max_hp // 4 attacker.current_hp = max(0, attacker.current_hp - recoil) if attacker.current_hp == 0: return 1 - attacker_idx # ターン終了処理 for attacker_idx in move_order: attacker = pokes[attacker_idx] if attacker.strategy == PokeStrategy.LEFTOVER: # たべのこしが発動 # 回復量は切り捨て(切り捨てて0になるケースは1になるが、LV50戦では発生しないため未実装) attacker.current_hp = min( attacker.max_hp, attacker.current_hp + math.floor(attacker.max_hp / 16), )
simulate関数にパーティ2つを与えて1000回呼び出し、パーティの勝率を計算します。
混合戦略ナッシュ均衡の計算
パーティの全組み合わせ(1292C2=833986通り)で上記のシミュレーションを行い、パーティ1つを1つの戦略とする利得行列を作成します。「求められた解」に示した利得行列の、全パーティが含まれるバージョンであり、1292×1292サイズの行列となります。 利得行列を入力とし、Nashpyというライブラリを用いて線形計画法により、混合戦略ナッシュ均衡が求まります。計算時間は30秒程度です。
Nashpyの説明はこちらから。
ほとんどの戦略(パーティ)は他の戦略より完全に劣って選出確率が0となり、9つの戦略が正の確率を与えられ、有効であると出力されました。
検算してみる
修正: 反動ダメージは切り捨てではなく四捨五入のため、結果に変化がありますので具体的な計算結果は利用しないでください。申し訳ありません。
シミュレーションのコードは今回のために新規実装したもので、バグがあるかもしれません。代表的な例を1つ、検算してみました。 検算対象とするのは、ガラルヤドラン(チョッキ,H4,A252,B252,S0,A↑,S↓,最遅)とエルレイド(チョッキ,H4,A252,B252,S0,A↑)の対戦です。シミュレーションでは、ガラルヤドランの勝率が69.3%となり有利でした。 いずれもとつげきチョッキを持っているので、最初のターンからわるあがきを打ち合います。エルレイドが常に先攻です。
パーセントで簡易計算
まずは、最大HPに対するダメージの比率(パーセント)で簡易的に計算してみます。結論としては、ずいぶんシミュレーションと異なる結果になります。
著名なダメージ計算ツールを使います。
わるあがきのダメージ率は以下のようになりました。
2ターン経過後、残りHPは以下のようになります。急所はないものとしています。まだどちらも倒れません。
- ガラルヤドラン 13.6%~19.6% ((100-25(反動)×2-18.2×2)~(100-25×2-15.2×2))
- エルレイド 4%~11%
3ターン目、先攻のエルレイドが攻撃したところでガラルヤドランが倒れるかどうかが問題になります。
ガラルヤドランの残りHPが13.6%であれば、ダメージ15.2%~18.2%の範囲のどれでも倒れる、残りHPが19.6%であれば、どれでも倒れないということになり明確な解答が得られません。もしもガラルヤドランがここで倒れなければ、エルレイドに25%の反動が入りガラルヤドランの勝ちです。
問題を変形すると、(エルレイド→ガラルヤドランの攻撃)15.2%~18.2%の乱数を3回合計し、さらに(ガラルヤドランの攻撃2回の)反動の50%を加算したとき合計が100%以上となれば、ガラルヤドランが倒れ、エルレイドの勝ちといえます。
手計算は少し面倒なので、さらに少し変形してChatGPT o3に検討してもらいましょう。
数学の問題です。15.2~18.2の一様分布乱数を3つ合計した値が、50以上になる確率を計算してください。
結果は52.5%でした。この計算結果から考えると、エルレイドのほうがわずかに有利となります。これはシミュレーションの結果とずいぶん違います。
次に急所を考慮しましょう。急所率は1/24のため、2回以上急所が出ることは極めて低確率なので1回だけ出る想定をします。
ガラルヤドランが2ターンで1回以上急所を出す確率が8%(=1-(23/24)2) あり、その場合は2ターン目にエルレイドを倒せる可能性があります。通常のダメージ率19.5~23.0%と、それを1.5倍した急所ダメージ率29.25~34.5%の合計が50%以上となれば、エルレイドが倒れ、ガラルヤドランの勝ちとなります。
ChatGPT o3で再び検討します。
数学の問題です。一様分布乱数19.5~23.0と、一様分布乱数29.25~34.5を足した値が50を超える確率を計算してください。
結果は95.7%でした。
エルレイドが1回急所を出しても、2ターンでガラルヤドランを倒すことは不可能です。(最大乱数18.2%の(1+1.5)倍が50未満)
これらを場合分けすると次のようになります。
- ガラルヤドランが2ターン目に勝ち: 8%*95.7%=0.07656
- そうならない: 0.92344
合計すると、ガラルヤドラン勝ちは51.5%となります。ここで考慮していない、エルレイドが3ターンのうち1回以上急所を出すケースではエルレイドに少し有利になり、ガラルヤドランの勝率は51.5%未満となります。シミュレーションではガラルヤドランの勝率が69.3%となっているので、大きく結果が違います。
緻密に計算
パーセントを使った簡易的な計算ではシミュレーションと大幅に違いました。その原因は、ダメージの範囲を「一様分布乱数」で仮定したことです。
ダメージ計算ツールで計算結果の詳細を見ると、ダメージが26になる確率は3/16である一方、ダメージが31になる確率は1/16となっています。16段階の乱数により、整数26~31(6通り)の範囲のダメージが決まるため、一様分布ではありません。

一様分布でない乱数を正確に処理し、エルレイド→ガラルヤドランの攻撃が3回あった場合のダメージの合計の分布は、有限マルコフ連鎖を用いて以下のように求めることができます。
# 3ターン後の合計ダメージの分布を計算 cur_dist = {0: 1.0} # ダメージ→確率の辞書。最初は合計ダメージ0の確率が1。 for turn in range(3): next_dist = defaultdict(float) # このターンでダメージを受けた後の分布。初期値は0。 for total, prob in cur_dist.items(): # 現在の合計ダメージと、その確率のペア。 for critical, c_prob in [(False, 23/24), (True, 1/24)]: # 急所に当たるかどうかの分岐 for r in range(16): # ダメージの16段階の乱数 damage = calc_damage(poke1.level, 50, poke1.a, poke0.b, critical, r) # 急所・乱数の条件を与えてダメージを計算 next_dist[total + damage] += prob * c_prob * 1/16 # ダメージがtotal+damageになる確率は、現在までのダメージがtotalである確率にこのターンでダメージdamageが出る確率を掛けて求める cur_dist = next_dist # 合計ダメージがX以上となる確率を表示 cum_prob = 0.0 for damage in reversed(sorted(cur_dist.keys())): # ダメージ138, 137, ...の順にスキャン cum_prob += cur_dist[damage] print(f"damage={damage},prob={cum_prob:.2f}")
この計算の結果は以下のようになります。
damage=138,prob=0.00 ...(中略)... damage=92,prob=0.12 damage=91,prob=0.13 damage=90,prob=0.15 damage=89,prob=0.19 damage=88,prob=0.25 damage=87,prob=0.33 damage=86,prob=0.44 damage=85,prob=0.56 damage=84,prob=0.69 damage=83,prob=0.80 damage=82,prob=0.88 damage=81,prob=0.94 damage=80,prob=0.98 damage=79,prob=0.99 damage=78,prob=1.00
例えばダメージ90以上になる確率は0.15です。ガラルヤドランの最大HPは171で、最初の2ターンでわるあがきの反動として(floor(171/4)=)42×2ダメージを受けます。エルレイドからの攻撃で171-42×2=87以上のダメージを受けると倒れます。そしてその確率は0.33と算出されています。この確率はガラルヤドランが負ける確率なので、ガラルヤドランが勝つ確率は0.67となります。シミュレーション結果の69.3%にかなり近い結果が得られました。残りの差は、ガラルヤドランが急所を出して2ターン目で勝利するケースです。
たった3ターンの攻防であっても、ダメージの範囲を一様分布で雑に処理すると本来の正解とは大きく異なる結果が得られることがわかりました。仮想敵のパターンが極めて多い通常のバトルではここまで緻密な計算は不要かもしれませんが、選択肢が少ない環境では考察に影響を与えます。
より厳密に求めるには
今回は実装しませんでしたが、努力値配分を4ずつ変えた細かい調整をするためには以下の方針が有効と期待されます。
- 勝率計算をモンテカルロシミュレーションではなく、有限マルコフ連鎖により厳密に求める
- わずかな努力値配分の差を勝率に反映するには、1000回程度のシミュレーションでは不十分な可能性が高いです。
- Double Oracleアルゴリズムにより、勝率計算を行うパーティを限定する
結局どのポケモンを育成するか?
シミュレーション結果として、単一の最強のパーティはなく、9つの候補があることがわかりました。全参加者が選出確率通りにさいころを振って使用パーティを決めれば、本当にどのパーティでも勝率50%になりますが、実際には偏りが出ますし、この候補にないパーティが使用される可能性もあります。これ以上は、純粋なシミュレーションでは求まらない、心理的要素を考慮するしかありません。
私の結論は、「ヤドラン(ガラル),チョッキ,H4,A252,B252,S0,A↑,S↓,最遅」の選択でした。理由は以下の通りです。攻撃種族値最大のエルレイドはわかりやすい選択肢であり、これに対して有利であること。利得行列内で明らかに苦手な(勝率がほぼ0の)相手が1パーティしかなく、参加者が特定のパーティに偏ったときに大きく損をするリスクが低いこと。一定(ナッシュ均衡における1%より多い)の参加者がたべのこしを好むと想定し、たべのこしを使う唯一の選択肢に有利であること。
特性はマイペースを選択します。クイックドロウは不利と想定したためです。シミュレーションに入っていない、ピクシーのメロメロボディの対策のため性別は♀を選択します。ピクシーは♀が多いこと、頻繁に目にするであろうエルレイドは♂限定であるため♀を選ぶインセンティブがあると考えたためです。
この記事は大会前に書きました。実際の結果は次の記事にて。
後日修正: わるあがきの反動
わるあがきの反動を、最大HP/4の切り捨てで計算していましたが、本来は最大HP/4の四捨五入でした。再計算した結果を示します。

| 選出確率 | パーティ |
|---|---|
| 21.99% | ブリムオン,チョッキ,H60,A252,B196,S0,B↑,S↓,最遅 |
| 15.11% | ヤドラン,チョッキ,H4,A252,B252,S0,B↑,S↓,最遅 |
| 14.46% | エルレイド,チョッキ,H4,A252,B252,S0,A↑ |
| 11.26% | ヤドラン,チョッキ,H252,A4,B252,S0,B↑,S↓,最遅 |
| 10.20% | ヤドラン(ガラル),チョッキ,H4,A252,B252,S0,A↑,S↓,最遅 |
| 7.56% | ヤドラン,たべのこし,H252,A4,B252,S0,B↑,S↓,最遅 |
| 5.74% | ルカリオ,チョッキ,H4,A252,B252,S0,A↑ |
| 4.86% | ブリムオン,チョッキ,H252,A4,B252,S0,B↑,S↓,最遅 |
| 3.07% | ブリムオン,チョッキ,H252,A4,B252,S0,A↑,S↓,最遅 |
| 3.00% | ヤドン,チョッキ,H4,A252,B252,S0,B↑,S↓,最遅 |
| 2.76% | ヤドラン(ガラル),チョッキ,H4,A252,B252,S0,B↑,S↓,最遅 |
大枠としてブリムオン・ヤドン→ガラルヤドラン→攻撃力高い組→ブリムオン・ヤドンという3すくみは維持されていますが、攻撃力が高いポケモンとしてエルレイドの他にルカリオが出てきています。 手計算したガラルヤドラン(チョッキ,H4,A252,B252,S0,A↑,S↓,最遅)vsエルレイド(エルレイド,チョッキ,H4,A252,B252,S0,A↑)のケースでは、以前の計算ではガラルヤドランが少し有利でしたが、修正したシミュレーションではわずかにエルレイドがわずかに有利に変化しています。ダメージ%での大雑把な計算では、わるあがきの反動を25%として処理しているため影響はありませんが、厳密な計算ではガラルヤドランが受ける反動が42ではなく43になるため、エルレイドの3回目の攻撃でガラルヤドランが倒れる確率は33%から56%に変化します。ダメージ1の差が結果に大きく影響する箇所になっており、このケースの結果は大きく変化しました。
ダメージの仕様確認には注意していきたいと思います。