2026年1月26日、ごりちゅう(X: srtbprofessor83)さん主催の「メタル化・テラスタル装甲2」に参加しました。「ラスターカノン」のみを覚えたポケモン1体でポケモンSVのオンライン対戦を行います。
イベントの情報はこちら。
フフ…バカめ…罠カード発動!!
— ごりちゅう (@srtbprofessor83) 2026年1月20日
#メタル化・テラスタル装甲2 !
1月26日(月)に #仲間大会 やります、ラスターカノンするだけの大会です。
画像使い回しかよと思われそうですがですが1時間のみ、技固定の1on1なので気軽に考察、参加してくれると嬉しいです。 pic.twitter.com/5LbL5eBLp5
私のパーティ
フリージオを採用しました。フリージオ、特性ふゆう、持ち物こだわりメガネ、鋼テラスタル、努力値H252C152D100S4、性格ひかえめです。
結果
8勝8敗でした。フリージオ戦が10回、ほかサザンドラ・テツノコウベ・クワガノンでした。全員、初手鋼テラスタルでした。
素早さで負けているケースがほとんどで、確定数が同じようだが先制されて負けるというケースが多くありました。また、特防ダウンを早めに引かれて負けというケースもあり、相対的に不運でした。Sを4だけ振ることで無振り相手には勝てるという想定でしたが、もう少し多めに振られていた方が多いということだと考えられます。
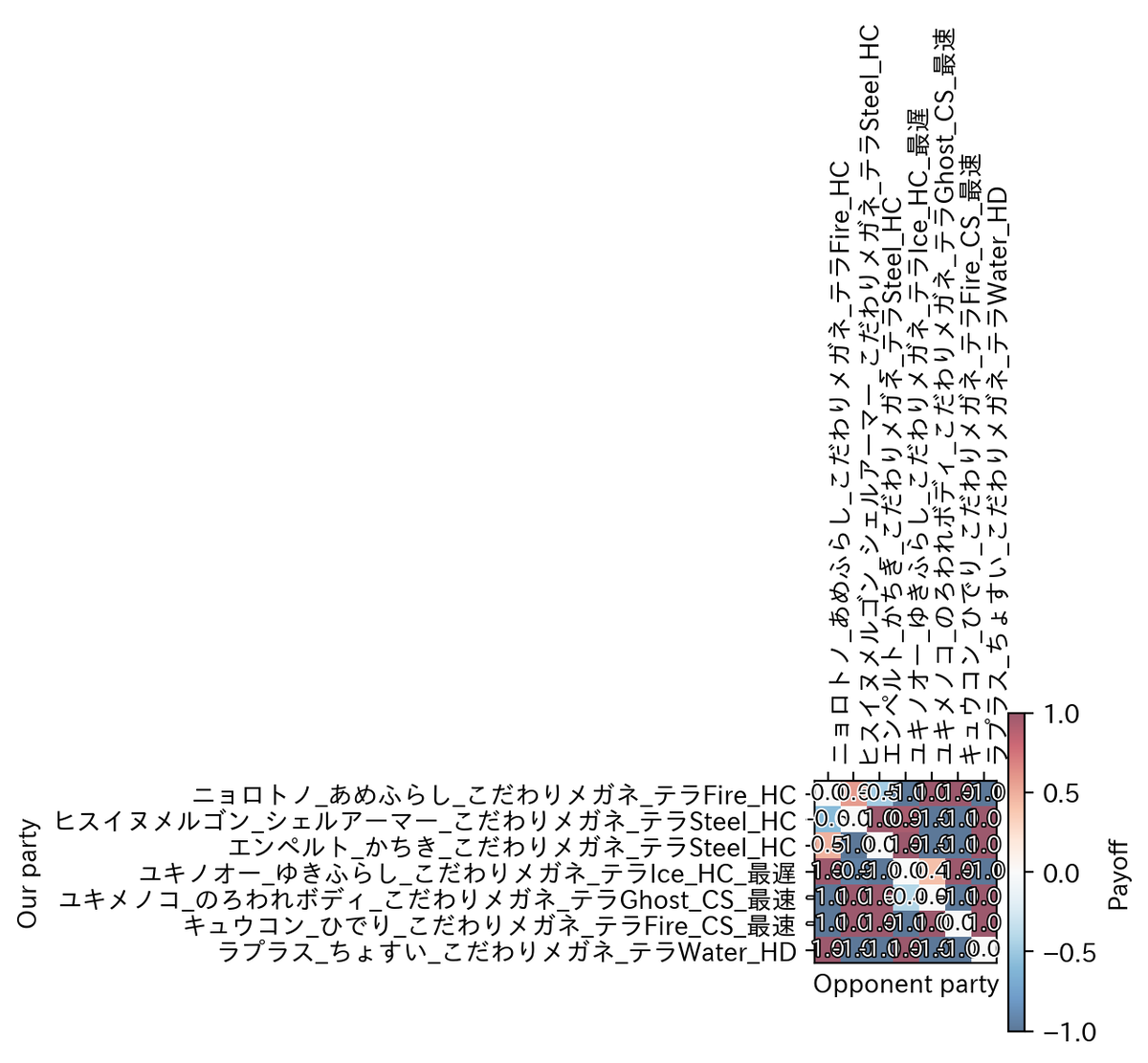
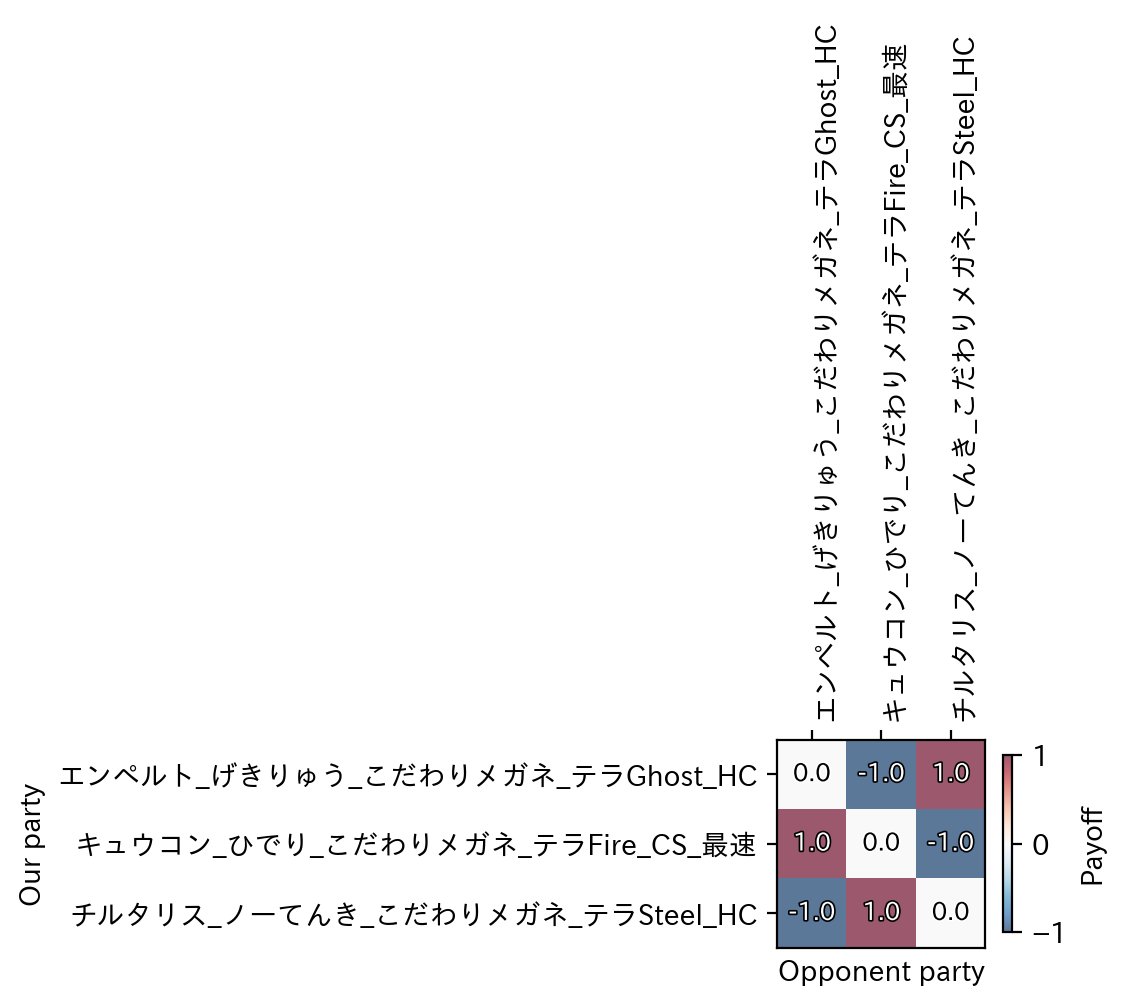
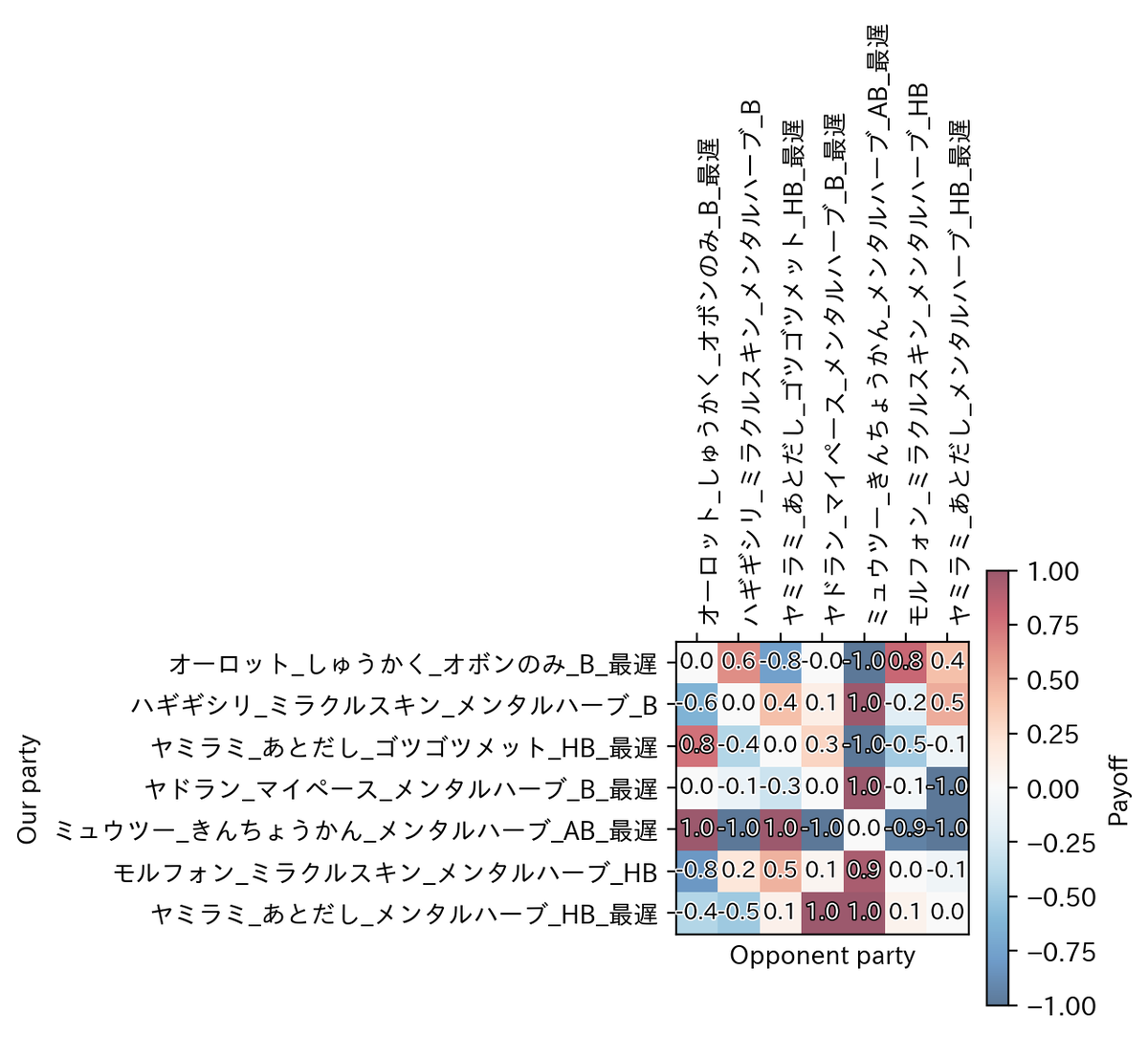
環境考察
「ウェザーボール1on1」の時に開発した、対戦中の選択肢を含んだシミュレーション機構を発展させました。
ルール
ルールは以下の通りです。
- ポケットモンスター スカーレット・バイオレットで対戦します。
- オンライン対戦の「シングルバトル ノーマルルール」を採用します。すなわち、レベル1~100のポケモンが参加可能ですが、バトル中のポケモンのレベルは50に統一されます。
- パーティにはポケモンを1体のみ登録できます。
- ポケモンには、技「ラスターカノン」のみを覚えさせます。「ラスターカノン」を覚えられないポケモンは参加できません。
- 使用可能ポケモンは、主催者によりリストで与えられています。
- テラスタルが許可されています。
- 特性・持ち物は自由に選択できます。
使用可能ポケモンリストは、以下のポケモンと、その進化前です。 カメックス・アローラサンドパン・アローラダグトリオ・エアームド・キングドラ・バクーダ・ブーピッグ・ドサイドン・ランクルス・シビルドン・フリージオ・ゴルーグ・サザンドラ・ブロスター・メレシー・ドデカバシ・クワガノン・シロデスナ・ジャラランガ・キョジオーン・グレンアルマ・リククラゲ・クエスパトラ・ミミズズ・キラフロル・イダイナキバ・スナノケガワ・テツノコウベ・クレベース
技術的変更点
対戦中の行動の選択肢として、「初手テラスタル」「テラスタルしない」の2択を設定しました。 作戦を練るコーディングエージェントとしてClaude Codeを用いました。従来はCodex + GPT系列のモデルでした。今回のモデルは、レートリミットの都合上モデルを使い分け、初期考察にClaude Sonnet 4.5、ループに組み込んでパーティ候補を出すフェーズにClaude Haiku 4.5を用いました。 HP・特防の努力値配分ですが、LLMに任せたままだと種族値を気にせずHP252に振るだけという挙動になりやすいです。そのため、HPと特防の努力値合計とポケモンの種族を与えると、特殊耐久が最大になる配分を計算するAgent Skillsを作成し、パーティの候補を提出する前に必ず使用させるようにしました。
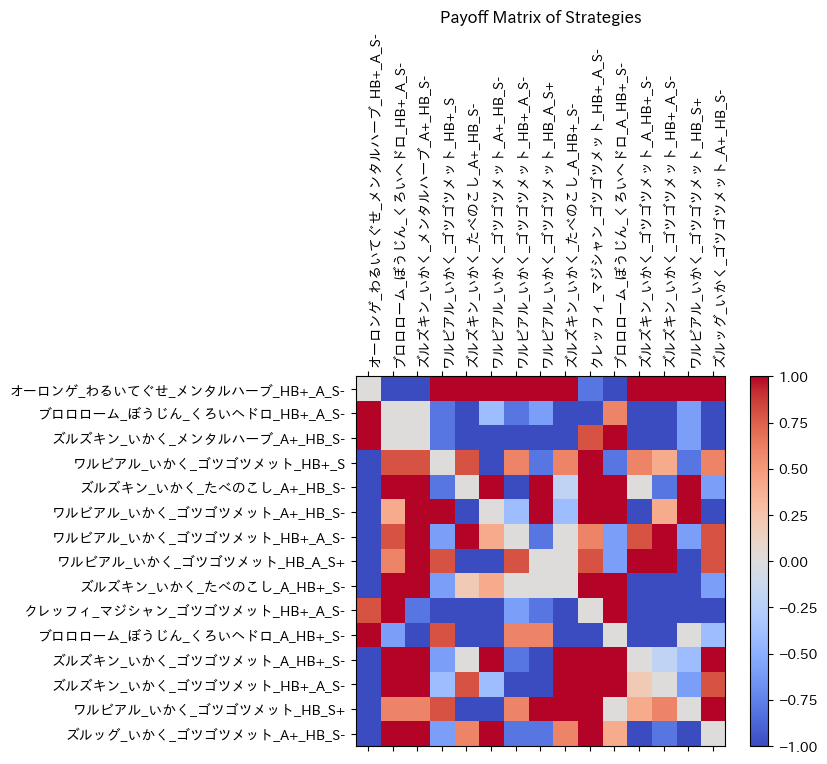
最適化結果
56パーティが試され、結果として以下の2つのパーティが等しく最適(勝率50%ずつを分け合う)という結果が出ました。
フリージオ、特性ふゆう、持ち物こだわりメガネ、鋼テラスタル、努力値H252C150D100S8、性格ひかえめ フリージオ、特性ふゆう、持ち物とつげきチョッキ、鋼テラスタル、努力値H252C96D96S60、性格おだやか
努力値について、特攻(攻撃系パラメータ)を中途半端な値で出力してきたのは、今までの考察システム開発で初めてです。今まで使用していたGPTと、今回使用したClaudeの差異かもしれません。シミュレーション上良い結果ですが、正確な数値に根拠はない可能性が高いです。特攻種族値最大のクワガノンでこれらを上回れないかなど、手動で少し追加考察をしましたが、上回る方法を見つけられませんでした。 テラスタルの有無は両方シミュレーション中に試すという仕組みになっていますが、使用可能ポケモンに鋼技を1/4倍で受けられるタイプは存在せず、鋼テラスタルをしないという選択肢は存在しないものと思われます。
最終的に採用したのはこだわりメガネ型です。ターン数が少なくて済むので、ラスターカノンの追加効果や回復系アイテムで妙なことが起こりづらいと期待できるためです。ただし、努力値は4n+8になるたびに実数値が上がる仕組みなので、素早さ8などは不自然です。そのため、手動で調整して、最終的に冒頭に書いた通り、「フリージオ、特性ふゆう、持ち物こだわりメガネ、鋼テラスタル、努力値H252C152D100S4、性格ひかえめ」となりました。
おわりに
主催のごりちゅうさん、対戦してくださった方ありがとうございました。乱数での特防ダウンが効くので、(A連打するだけではあるのですが)最後まで気の抜けない戦いになるのが面白かったです。 技術面では、今までで参加した中で最もシンプルな殴り合いのルールとなり、LLMを用いたヒューリスティックよりも数値レベルの最適化問題としてとらえたほうが良かったように思われます。現状の枠組みにとらわれず、様々なアイデアの検証を進めていこうと考えています。